Измеряется сила притяжения. Ускорение свободного падения на Земле. От плотности пород земной коры
Гравитация является одним из самых загадочных физических явлений. Ни о каком ином явлении не высказано, не написано, не защищено диссертаций, не присвоено академических званий и Нобелевских премий, как по гравитации.
Любые представления исторически обусловлены. Время меняет задачи, стоящие перед обществом, а это заставляет, как правило, менять и представления о тех или иных явлениях. Не является исключением и явление гравитации. Не могут не отличаться представление о гравитации у строителей египетских пирамид и у путешественников по космическому пространству.
Проанализировав собранные в то время данные, Лаплас решил, что «гравитация» распространяется быстрее света, по крайней мере на семь порядков! Недавние измерения еще больше изменили скорость гравитационного расширения - как минимум на 11 порядков быстрее скорости света.
Существует подозрение, что «гравитация» распространяется в мгновение ока. Но если это действительно так, то как это исправить - в конце концов, измерение теоретически невозможно без ошибок. Значит, вы никогда не знаете, конечная или бесконечная скорость. И мир, в котором у нее есть граница и мир, в котором она нет, - это «две великие различия», и мы никогда не узнаем, в каком мире мы живем! Вот граница научного знания. Принятие той или иной точки зрения является вопросом веры, совершенно иррациональным, вопреки логике.
2.Ньютоновское понимание гравитации
В ньютоновской гравитационной теории гравитация фактически полностью ассоциирована с силой тяжести или силой веса. Сущность гравитации по Ньютону в том, что к телу приложена сила - сила тяжести (в условиях Земли она обычно называется силой веса). Источник этой силы - другое или другие тела. Никакого гравитационного поля, фактически, нет. Гравитация есть прямое взаимодействие между телами. Это взаимодействие определяется Законом Всемирного Тяготения Ньютона. Никакого особого гравитационного пространства не существует. Гравитационное поле носит условный характер и служит лишь для удобства расчетов, никакой физики за этим понятием нет.
Сзади, изменения гораздо более тонкие. Мультимедийный дисплей также может отображать информацию о продольном и поперечном ускорении, крутящем моменте или мощности. Кроме того, новое рулевое колесо было сплющено на дне, доступное более чем в 100 вариантах. Для облегчения загрузки багажа багажник автоматически поднимается при открытии крышки.
Как и ожидалось, передовой моторный ряд будет сопровождать обновленный родстер. Мир, который мы создали, - это процесс нашего мышления. Его нельзя изменить, не изменяя нашего мышления. Если вы не можете объяснить что-то шестилетнему ребенку, то вы даже не понимаете. Тот, кто говорит, что это невозможно, не должен мешать тому, кто не верит в это. Как странно наша ситуация, дети Земли: все здесь для короткого визита; никто не знает почему, но иногда она думает, что чувствует. Вы не можете обвинять силу тяжести, когда любовь теряет вас.
В земных условиях, например, при расчете статических конструкционных нагрузок, это удобное и наглядное представление.
3.Гравитационные явления в современном мире
Современный мир далеко вышел за рамки круга явлений, в которых сформировались ньютоновские гравитационные представления. Уже в начале прошлого века Альберт Эйнштейн обратил внимание на то, что даже явление в обычном лифте плохо согласуются с представлениями Ньютона. Это, а также релятивистский пунктик привели его к новому пониманию гравитации, отраженному в так называемой Общей теории относительности.
Бог не заботится о наших математических трудностях. Он интегрируется эмпирически. - Альберт Эйнштейн. Это не просто большой шаг, это на самом деле другой подход с концептуальной точки зрения. Если мы хорошо мыслим, сила тяжести является одной из самых слабых сил в природе, в которой мы находимся. И гравитационная линза еще слабее. Но использование современной, особенно чувствительной, фотоэлектрической и спектроскопической аппаратуры, привязанной к нашим телескопам, и особенно развитой, является удивительной помощью для обнаружения темной материи.
Сейчас общепринято, что ОТО есть гравитационная теория космологических масштабов и релятивистских движений. Но в масштабах макро- и мезомира, т.е. в области земной, планетарной (небесной) механики и космонавтики, ОТО не имеет смысла использовать и ничего нового эта теория дать не может. А если и дает, то только поправки в каких-то уж очень высоких приближениях. Поэтому мы остановимся на более детальном рассмотрении ньютоновских гравитационных представлений.
Темная материя была достаточно сложной. Вы не можете знать, как началась Вселенная, потому что доказательств не было, как и не для Аристотеля, Птолемея и Коперника. Они не смогли возродить пространство для его реабилитации; вы не можете пойти в прошлое. Все, что вы могли сделать, это наблюдать настоящие явления - эти галактики с галактикой-галактикой - и пытаться найти математику для их перемещения. Все, что вы можете сделать, это попытаться спасти появление, если это была ваша идея науки.
Ньютон воображает гравитацию как силу, действующую на пространство, а уравнения Эйнштейна в теории общей теории относительности считают гравитацией как пространственное свойство. Материя контролирует кривизну пространства, а пространство, в свою очередь, говорит о том, как двигаться. Вы должны двигаться, принимая во внимание свойства пространства. Первая демонстрация эффективности теории общей теории относительности была установлена в объяснении эллипса Меркурия вокруг Солнца. Вытеснение планеты Меркурий на изменяющемся эллипсе, вращающемся подобно спирали вокруг Солнца, перемещая перигелий, было первой проверкой теории общей теории относительности.
Одно из главных явлений, которое оказалось в центре рассмотрения механики в последние десятилетия, стало явление невесомости. Конечно, явление невесомости встречалось и ранее. Но было оно кратковременным и не осознавалось как некое особое механическое явление. Падает камень с Пизанской башни, ну и падает. Какая тут невесомость. Но развитие космонавтики вывело явление невесомости на первый план, была осознана его высокая значимость. Невесомость постепенно входит в разряд производственных и технологических факторов.
Вместо относительно стабильного эллипса, как и другие планеты, орбитальный оборот планеты Меркурий вокруг Солнца представляет собой эллиптическую спираль. Причиной является слишком близкий Меркурий к Солнцу. Отклонение светового луча от звезды, когда оно проходило вблизи Солнца до полного затмения, было второй проверкой теории общей теории относительности.
Сегодня мы называем это гравитационной линзой, что многое может сказать, и в картировании темной материи вокруг галактических стай. Человеческий глаз видит небольшой диапазон спектра электромагнитных волн: красно-желто-синяя линия. Но давайте последуем за Ричардом Панеком.
Но обращаясь к ньютоновским механическим представлениям, мы вдруг обнаруживаем, что этого понятия в механике Ньютона, фактически, не существует. По ньютоновским представлениям сила тяжести связана с гравитацией. Но вдруг оказалось, что это совсем не так. Покажем это.
Представим себе парашютиста на самолете перед броском в небо. Он стоит перед дверным проемом и находится в гравитационном поле, на него действует сила веса. Так считается по Ньютону. Но вот он делает шаг за дверь.Ясно, что гравитационное поле при этом не изменилось. И сила веса также не могла измениться. Но парашютист перешел в невесомое состояние, и потерял свой вес, неожиданно исчезла сила тяжести. Но ведь гравитационное поле не исчезло, оно каким было, таким и осталось. Поэтому очевидно, что и вес внутри самолета не был связан с гравитацией.
Астрофизик Джордж Гамов и его ученики пришли к выводу, что некоторые химические элементы в сегодняшней вселенной происходят с первых дней ее образования. Некоторое излучение, предположительно из-за большого взрыва, все еще циркулирует во Вселенной. Было также обнаружено, что самые легкие элементы, такие как водород, дейтерий и гелий, были первыми элементами во Вселенной, а другие более тяжелые элементы позже сформировались. Исследователи утверждают, что в ядерном процессе в звездах образуются более тяжелые элементы, чем гелий, и легче, чем железо, а самые тяжелые элементы были образованы взрывами сверхновых.
Иногда говорят, что сила веса вовсе не исчезла, а появилась (фиктивная) сила инерции, которая и уравновесила силу тяжести, так как парашютист стал двигаться ускоренно. Именно поэтому сам парашютист никакой силы веса не ощущает.
Правильно, в системе отсчета, к примеру, судейской коллегии, размещенной на земле, парашютист движется ускоренно. Но представим, что вместе с парашютистом выпрыгивает и фоторепортер, который снимает полет и действия парашютиста. И по отношению к этому фотографу парашютист может двигаться вверх, вниз, может стоять на месте. И где же тогда пресловутая сила инерции, связанная с ускоренным движением парашютиста? Как можно реальную силу, каковой, якобы, является сила тяжести, уравновесить фиктивной силой инерции, связанной с ускорением, если ускорение может иметь самый различный характер в зависимости от наблюдателя или вообще отсутствовать? Если принять, что земная судейская система отсчета более «правильная», чем система отсчета фотокорреспондента, то нужно доказать, что судейские фотоаппараты, судейские часы или дальномеры лучше, чем таковые же фотокорреспондента.
Но этот гигантский путь - это всего лишь небольшой поклон на его орбите. Для Солнца требуется тысячи лет, чтобы сделать одну вращение вокруг галактики. Таким образом, это было измерение галактики Андромеды. Идя в темную комнату, Рубин ждал, чтобы обнаружить аспект планет в нашей солнечной системе: чем дальше от Солнца, тем медленнее планета движется по своей орбите - так же, как Ньютон предсказал с универсальным законом гравитации. планета в четыре раза дальше от Солнца, чем другая планета будет двигаться с половиной скорости.
Планета на расстоянии в девять раз дальше будет двигаться на треть от скорости. Плутон находится на расстоянии сто раз от Солнца, чем от Меркурия, поэтому он будет двигаться и делать это с десятой скоростью Меркурия. Если вы построите эту зависимость между расстоянием и скоростью, тем медленнее скорость - вы получите постепенное снижение, нисходящей кривой.
Так как это невозможно доказать, то приходится признать, что силы инерции есть фикция, а, следовательно, фикцией являются и силы тяжести, силы веса и вообще, все гравитационные силы, их просто не существует.. И парашютист в свободном падении движется именно свободно , т.е. без воздействия на него каких-либо сил (влиянием атмосферы пренебрегаем).
Но график Рубина для галактики Андромеды был прямой. Казалось, что Плутон двигался с той же скоростью, что и Меркурий. Это не заняло много времени, и радиоастрономы достигли такого же результата. Гравитация примерно в десять раз выше. Другой физик Джим Пиблс начал использовать один из самых мощных компьютеров в то же время в том же году и попытался смоделировать галактику с 300 фигурами в ротации, чтобы получить фигуру спиральной стрелки, уже известную, Вскоре после этого он также достиг тысячи вращающихся тел.
Физики не хотели прерывать сбор новых данных, но «результаты настолько поразительны, что мы хотим представить предварительную оценку». Измеренные кривые вращения также были плоскими. В этот раз измерения радиоастрономии были согласованы. Это означало, что быстрое вращение галактик доказало одно: галактики не умирали молодыми. Но даже самые вопиющие критики были трудно противоречить из-за однородности данных.
Тогда что же произошло с парашютистом, когда он делал свой шаг за борт самолета? А он вовсе не нагрузил себя таинственной фиктивной силой инерции, уравновесившей силу тяжести. Нет, он, наоборот, избавился от единственной реальной силы, действовавшей на него. Эта сила исходила от опоры, от пола самолета. И когда он освободился от нее, сделав шаг за пределы самолета, он и стал невесомым, стал свободным , на него перестали действовать какие-либо силы.
Проблема для астрономов заключалась в том, что они не могли этого видеть. Не с глазами, а не с традиционным оптическим телескопом, а не с телескопом, который мог видеть на любой длине волны света. В этом случае еда не «отсутствовала». В середине двадцатого века астрономы обнаружили, что, глядя дальше по всему электромагнитному спектру, т.е. за пределы видимого спектра, во Вселенной наблюдалось гораздо больше. И теперь, если бы вы были Верой Рубин, спросите вы, как вы можете видеть больше, чем электромагнитный спектр, - и за пределами самого зрения?
Таким образом, нет никаких гравитационных сил. Есть силы, действующие на человека, на камень на земле, на космонавта во время активного участка полета со стороны опоры. Если удалить опору, человек или камень станут свободными, невесомыми. Но силы, которая действует со стороны опоры на человека или камень никакие не гравитационные. Это обычные силы упругости, имеющие электрическую или, более обще, электромагнитную природу. А тело человека (подошвы) или камень, в свою очередь, обладают упругостью, и возникнет сила противодействия, направленная от подошв или камня к опоре. И эта сила тоже имеет электромагнитную природу. А где же гравитационные силы? Мы их не видим. Их нет.
Расстояния до небесных объектов. Галактика на переднем плане - более полезная, чем звезда на переднем плане - могла бы служить в качестве более сильной линзы силы тяжести. Было доказано, что гравитационный эффект темного объекта на переднем плане заставляет свет другого объекта в фоновом режиме казаться ярче. Такие открытия умножились с года.
Недавние наблюдения, даже с наземными телескопами, включают отдаленные и квазарные галактики, которые существовали уже тогда, когда Вселенной было всего один миллиард лет. Таким образом, изучение вселенной уже может быть сделано в течение как минимум 12 миллиардов лет назад. Отныне, в прошлое, мы также можем посмотреть, как эта вселенная развивалась за тот же период.
Вот центральное, главное, фундаментальное утверждение, которое вытекает из космического опыта человечества: гравитационных сил нет . Запишем это самыми крупными буквами и станем на этом фундаменте создавать новую механику, механику космической эры.
4.Природа гравитации в свете опыта и представлений космонавтики
Но если нет гравитационных сил, нет силы тяжести, то значит нет и гравитации? Нет, это не так. Гравитация, конечно, существует..
Из распределения галактик ясно, что мы имеем относительно однородную и изотропную вселенную. И от того, насколько далеко нам удалось проникнуть в то, чем была вселенная раньше, - чтобы смотреть на большее расстояние - мы обнаруживаем, что существующая структура уже существовала, когда вселенная имела только 10% своего возраста.
Чтобы проникнуть во вселенную, нам нужно измерить космические расстояния. Первый метод - определение звездного параллакса. Со вторым методом цефеиды достигают 130 миллионов световых лет. Цефиды используются с диаграммой яркости периода и могут достигать 1000 световых лет. Настоящая космическая свеча.
Но природа ее совсем иная. Она вовсе не силовое взаимодействие между телами. Никакого силового взаимодействия между Солнцем и Землей, между Землейи Луной, между Землей и космическим кораблем, между Землей и камнем на ее поверхности нет.
Гравитация есть свойство . Свойство это состоит в изменении характера пространства вокруг гравитирующего тела. Всякое тело окружено некоторым ореолом, нимбом измененного пространства. Этот нимб тело носит при себе как нимб вокруг головы святого или атмосфера, ионосфера, магнитосфера вокруг Земли.И оторваться от тела в «самостоятельное плавание» этот ореол не может. Он привязан навечно к телу и перемещается вместе с ним.
Мы поговорим немного о методе звездного параллакса. Углы, полученные при таких расчетах, очень малы. Таким образом, для других более длинных звезд получаются еще меньшие параллаксы. Теперь мы можем понять еще одну причину, из-за которой в прошлом даже для астрономов невозможность измерения звездного параллакса была научным аргументом против гелиоцентризма. Это был точно Тихо Браге, против Коперника.
У каждого сорта 60 минут. Это означает, что круг можно разделить на равные части - то есть за столько секунд. Звездный параллакс измеряет доли секунды. Солнце и Луна видны под углом в половину градуса или 30 минут арки. Никакая планета, видимая невооруженным глазом, превышает одну минуту дуги. Одна секунда дуги будет рассматриваться как монета диаметром 1, 8 см на расстоянии 4 км. Действительно, оптический прибор, оснащенный таким разрешением, необходимым для такого наблюдения, должен быть очень современным.
Вот тут мы можем сразу же сопоставить свойство этого нимба со свойствами электромагнитного поля. Электромагнетизм имеет два заряда, положительный и отрицательный. Предположим, что мы имеем электронейтральный атом или молекулу. Тогда электрического поля, никакого электромагнитного нимба нет. Но вдруг из него вылетела положительно или отрицательно заряженная частица. Он стал ионом, электрически заряженным телом, и вокруг него должен появиться соответствующий нимб - электрическое поле. Его не было, а теперь должно стать. И вот тут и возникает вопрос: с какой скоростью это возникающее из не6ытия поле будет распространяться в пространстве. Понятно, что мгновенно поле во всем пространстве установиться не может. Оно будет распространяться вдаль от атома, переходя все дальше и дальше. Мы видим, что электромагнитное поле является близкодействующим, оно может в принципе отрываться от источников поля, у него имеется некоторая скорость распространения. И связано это исключительно с существованием двух видов электрических зарядов. Более точно с изменением дипольного момента, на который нет закона сохранения. Электромагнитное поле имеет связанную скорость распространения, связанную с движением источников поля, заряженных тел, например, при движении электрического заряда или магнита, и автономную скорость распространения, не связанную с движением материальных тел, являющейся универсальной константой - скоростью света.
Должно быть, при виде неба в разное время года положение звезд в небе ближайших звезд изменилось над более дальними звездами. Так же, как мы выглянули из окна из движущегося поезда и увидели движущиеся объекты, которые двигались ближе, объекты все дальше двигались, а горы на горизонте казались совершенно неподвижными. Только когда сила телескопов увеличилась, было обнаружено, что звезды движутся друг к другу, особенно ближе всего к самому дальнему. Но это только с оптическими приборами, построенными только с середины девятнадцатого века.
Такие вещи случаются. И вот почему? Запишите параллакс с таким количеством десятичных цифр, именно потому, что точность измерения достигла третьего или четвертого знака после запятой. И это говорит нам и с какой точностью мы можем оценить расстояние до этой звезды.
В противорположеность электромагнетизму гравитации связана с источниками одного знака. Этот гравитационный источник, гравитационный заряд называется массой. Она всегда положительна и для нее существует закон сохранения... Более того, даже на массовый дипольный момент имеется закон сохранения - это, фактически, закон сохранения центра масс. Поэтому ниоткуда гравитационное поле возникнуть не может. Оно ввиду движения масс может как-то деформироваться, причем чем дальше находится точка наблюдения гравитационного поля от этих масс, тем больше требуется времени, чтобы эффект изменения поля был обнаружен. А на достаточном удалении от ограниченной системы масс она вообще может рассматриваться как единая нерасчлененная точечная масса, внутренние движения на достаточном удалении не могут изменить точечный характер этого поля. А на еще большем удалении гравитационное поле исчезает вообще, и никакими средствами мы его не сможем обнаружить. Пусть формально мы можем вычислить величину гравитационного поля Земли в другой галактике. Но очевидно, что это чисто теоретический артефакт. Отсюда прямо следует отсутствие пресловутых гравитационных волн , т.е. оторвавшихся от источников гравитационных полей. Гравитационных полей без источников не существует. Это в электромагнетизме испущенная электромагнитная волна теряет всякую связь с источником и есть «безисточниковое» электромагнитное поле. И в этом принципиальное отличие электромагнитного поля. Оно может действовать на любые расстояния. Так в наших оптических и радиотелескопах принимаются и воздействуют на приемникиэлектромагнитные поля, источник которых лежит в невообразимой дали, за миллионы и миллиарды световых лет. Электромагнитное поле - это поле с неограниченным радиусом действия в отличие от пространственно ограниченного гравитационного поля.
Заметим также, что существование гравитационных волн делает сомнительным принцип Галилея и самое существование инерциальных систем отсчета, а это уже ведет к катастрофическим последствиям для всей теоретической механики.
5.Гравитационные свойства пространства
Определим понятие свободного тела. Свободным телом мы будем называть тело, к которому не приложено никаких сил. Под силами, мы напоминаем и будем еще много раз напоминать, мы понимаем лишь воздействия электромагнитной природы. Ядерные и прочие микро- нано- фемто-силы вряд ли стоит рассматривать. А тела, на которые действуют силы (силы упругости, реактивные силы и иные силы электромагнитной природы) будем называть несвободными .
Определим понятие инерциальной системы отсчета. Инерциальной системой отсчета назовем такую систему отсчета, в которой свободные тела движутся равномерно и прямолинейно или покоятся. Иные системы отсчета будем называть неинерциальными . Отметим, что если у нас есть инерциальная система отсчета, то мы можем ввести и любое количество разнообразных неинерциальных систем отсчета, например, вращающиеся, колеблющиеся и т.д.
Определим теперь понятие галилеева пространства. Галилеевым будем называть пространство, в котором можно ввести инерциальную систему отсчета. Не во всяком пространстве можно ввести инерциальную систему отсчета. Если в пространстве нельзя ввести инерциальную систему отсчета, то такое пространство будем называть негалилеевым .
А теперь мы готовы сформулировать гравитационное свойство. Гравитационное свойство состоит в том, что в окрестности тела имеется область негалилеевости. В этой области невозможно ввести такую систему отсчета, чтобы в ней свободные тела двигались равномерно и прямолинейно или покоились.
Движения свободных тел будем называть естественными движениями . Там, где нет гравитации, там естественные движения могут иметь вид прямолинейный и равномерный. А гравитация приводит к тому, что естественные движения не могут иметь вид равномерный и прямолинейный. В гравитационном пространстве естественные движения гораздо более сложные. Это могут быть движения по окружностям, эллипсам, параболам,гиперболам и еще более сложным и замысловатымтраекториям. Сложнейшие траектории межпланетных космических аппаратов в свободном полете наглядно об этом свидетельствует. Почему это так - мы не знаем, гипотез не строим, а принимаем это как данную нам реальность..
Итак, теперь мы можем ответить на все поставленные выше вопросы в свете именно космического опыта.
1.Почему на орбитальном космическом корабле космонавт находится в состоянии невесомости? Ответ: не потому, что каким-то чудесным способом гравитационные силы уравновешиваются с мифическими инерционными. А по той простой причине, что он свободен, на него не действуют никакие силы .
2.Почему, если он свободен, он движется не прямолинейно, а по окружности? Ответ: потому что он находится в гравитационном поле, в области негалилеевости Земли, в которой движение свободных тел более сложное, в том числе может быть и круговое.
3.Почему Земля движется по кругу? Ответ: Земля является свободным телом. Никакие силы на нее не действуют. Но она находится в области негалилеевости (в гравитационном поле) Солнца. И свободное движение Земли является естественным движением - движением по кругу.
4.Какие силы действуют на камень на поверхности Земли? Одно из естественное движений камня в окрестности Земли, есть ускоренное падение в ее центр. Но поверхность Земли препятствует этому естественному движению путем приложения к камню силы, направленной вверх противоположно направлению естественного движения камня.. Сила эта не гравитационная, а обычная сила упругости, т.е. электромагнитной природы. Естественно, что по третьему закону Ньютона камень действует на свою опору с такой же силой, но уже вниз. Если вдруг опора исчезнет или потеряет твердость, то камень начнет естественное движение вниз, к центру Земли.
Отметим, что обычно силу, направленную от камня на опору - силу тяжести - считают активной силой, а силу от опоры к камню - силой реакции. В нашем представлении понятие активной силы и силы реакции поменялись местами. Активной стала сила от опоры к телу, силой реакции - сила от тела на опору. Это более отвечает механической логике. Активной является сила, которой можно управлять, а пассивной, силой реакции - это сила, возникающая ответно, автоматически. Силу опоры мы легко можем управлять. Опору можно убирать, ее можно делать более твердой, более мягкой и т.д. А сила от камня на опору при этом возникает автоматически. Например, когда камень лежит на ладони, то именно опорой мы можем манипулировать - держать камень, его подбрасывать и т.д. А действия камня на ладонь будут уже вторичными, ответными. Активную роль играет ладонь, а не камень.
6.Локальная галилеевость негалилеева пространства
У гравитационного поля есть уникальное свойство, резко отличающее его от электромагнитного. Самое удивительное, что это свойство теоретически до сих пор не освоено современной теоретической механикой, хотя практически оно используется, особенно в космонавтике, очень широко.
Если есть электромагнитное поле, то оно есть, и никакими преобразованиями систем отсчета его невозможно ликвидировать. Его компоненты, электрические или магнитные, могут преобразовываться друг в друга, но в области пространства, заполненного электромагнитным полем, оно есть в любой точке и в любой системе отсчета, у любого наблюдателя. У него есть инвариант.
Но совершенно иное мы имеем в гравитационном поле. Оказывается, гравитационное поле, т.е. область негалилеевости пространства, является одновременно локально галилеевым в каждой точке. Другими словами, можно исключить гравитационное поле в любой его точке и даже целой окрестности. Это следует из главного закона гравитации: в окрестности любого свободного тела имеется область галилеевости . Эта область может быть большой, глобальной, если свободное тело находится в галилеевом пространстве, или локальной, ограниченной, если само тело находится в негалилеевом, гравитационном пространстве.
Таким образом, мы приходим к важнейшему свойству гравитационного поля: гравитационное поле не абсолютно, а относительно. В любой точке гравитационного поля можно ввести такую систему отсчета, в окрестности которой его не существует.
До настоящего времени этот важнейший, центральный момент гравитации не был сформулирован в механической теории. А вот на практике он используется очень широко. Например, хотя Земля находится в области негалилеевости Солнца, но так как она свободное тело, то в ее ближайшей окрестности есть область галилеевости, в которой влиянием Солнца можно пренебречь. И если у Земли есть собственное гравитационное поле, то оно в этой окрестности накладывается не на поле Солнце, а на галилеево безгравитационное пространство, и мы можем рассчитывать в этой окрестности все движения так, как будто Земля находится сама по себе в галилеевом пространстве, и Солнца вообще не существует. Луна находится в области негалилеевости Солнца и Земли, но в окрестностях Луны мы можем учитывать только поле Луны, Космический корабль на орбите находится в области негалилеевости Солнца, Земли и Луны. Но при его свободном орбитальном движении внутри самой станции мы можем считать пространство галилеевым (собственное гравитационное поле станционной массы пренебрежимо мало) и в ней можно ввести инерциальную систему отсчета, в которой выполняется принцип Галилея. Причем это распространяется не только на внутреннее пространство станции, но и на ближайшую внешнюю окрестность ее. Это позволяет при стыковке с другим кораблем на близких расстояниях пользоваться механикой инерциальных систем отсчета и даже не принимать во внимание самое существование Земли и ее гравитационного поля. Это существенно упрощает расчеты движений и управлений. В то же время по мере удаления от станции все более и более существенными становятся негалилеевы характеристики окружающего пространства, ввиду лишь локальной его галилеевости. Поэтому при стыковке на «далеких рубежах» надо принимать во внимание гравитационное поле Земли, но можно не учитывать поле Солнца и Луны. К сожалению, существующая механика не дает инструментов учета гравитационного поля Земли в системе отсчета космического корабля и расчетчикам приходится переходить в земную систему отсчета, что, конечно, не удобно.
Итак, мы видим, сколь важную практическую значимость имеет принцип локальной галилеевости негалилеева пространства. И механическая теория, в которой этот принцип не имеет места, не может считаться пригодной для использования в космонавтике. А в ньютоновской механике этого принципа не существует. В этой механике гравитационное поле рассматривается только глобально, как правило, в единой выделенной «коперникианской» системе отсчета - системе отсчета центра масс. Мы назвали эту систему отсчета коперникианской, так как честь обнаружения «главных», выделенных систем отсчета, по праву, принадлежит Копернику. Но космонавтика требует отхода от коперникианской парадигмы, и такой отход происходит постоянно при навигационных космических расчетах. Использование локальных систем отсчета и есть отказ от парадигмы коперникианского глобализма при описании гравитационных полей. Вот почему новую механику можно назвать неньютоновской и некоперникианской или, может более правильно, неоптолемеевской.
Вновь отметим, в механике, связанной с механическими явлениями на поверхности Земли, ньютоновский подход достаточно удобен и эффективен, что показывает все развитие механики в течение столетий. Но в космонавтике этот подход вызывает большие трудности, о которых мы говорили выше. И новый подход максимально раскрывает логику механических процессов в космосе, открывает возможности более простого решения известных задач и формулировки новых.
7.Весомость как фундаментальное понятие механики
Мы показали, что во многих задачах механики, в частности, в задачах небесной механики,исчезают силы. Ведь небесная механика рассматривает, по преимуществу, свободные небесные тела, т.е. тела, к которым не приложены никакие силы.
Как известно, в ньютоновской механике понятие силы является фундаментальным, основным понятием. В механике оно даже не определяется, а берется из других наук, например, физики. Аналогично тому, как в механике не определяется понятия расстояния, оно является для нее фундаментальным и берется из геометрии.
Ясно, что в качестве фундаментальных понятий при аксиоматическом построении теории желательно использовать наиболее важные и широко используемые характеристики. Но парадокс состоит в том, что в разных масштабных областях механического мира таковыми становятся разные характеристики.
Например, ньютоновская механика наиболее хорошо приспособлена для описания явлений макромеханики, т.е. механических явлений в масштабах, сопоставимых с размером человека. И здесь сила является чрезвычайно важным понятием и использование ее в качестве фундаментального понятия вполне оправдано. Действительно, мы наглядно видим по напряжению жил силу лошади, тянущей фуру с дровами, мы видим силу натяжения лука, легко представляем силу на водиле паровой машины. Наконец, по напряжению своих мышц и напряженному дыханию видим силу веса поднимаемого нами бревна.
Но уже в области микромира силы становится плохо представимыми. И на первое место выходят иные механические характеристики, такие как энергия и действие. И соответственно возникают новые механические модели, теории, известные под общим названием «аналитической динамики». Это механики Лагранжа,Гамильтона, Пуанкареи т.д. Фактически, это разные «языки» механики, в которых удобно описывать свой класс и прежде всего масштабный уровень механических явлений. Хотя они в принципе эквивалентны, т.е. дают одинаковые решения одной и той же задачи, но в каждом языке есть класс задач, наиболее наглядно и просто решаемый именно в нем. Более того, распространение механики в область микромира, в квантовую область оказалось возможным именно в этих новых «энергетических» языках, например, в гамильтоновом языке, а для языка Ньютона так и не было построено расширение в квантовую область. Это уже показывает важность создания новых механических языков. Без построения целого класса таких языков на рубеже 19 - 20 веков, возможно, было бы невозможно создание механики микрочастиц, а без этого и создание всей техники, использующей их - электроники, атомной энергетики и т.п. Вот каково значение «языков механики». Ньютоновский язык послужил основой промышленной революции XVIII века и создания механических машин и механизмов. Неньютоновские, энергетические языки механики послужили базисом создания в двадцатом веке теории микромеханических процессов, каковая теория стала базой создания всей электроники, ядерной физики, лазерной техники и других областей техники в двадцатом веке.
Космонавтика, появившаяся в середине двадцатого века, до сих пор использует механический язык Ньютона, который разработан для иных масштабов механических явлений. Для космонавтики он плохо подходит. Отсутствие в этом языке такого центрального понятия как невесомость, а тем более «весомость», широкое использование таких уродливых и недопустимых в науке словечек как «перегрузка» (а что такое «грузка»?) с еще более ужасными словосочетаниями как «отрицательная перегрузка», «недоперегрузка» и т.д. говорит само за себя. Космонавтика и вообще, область мегамира нуждается в собственном, более адекватном языке. И очевидно, что использование понятия «силы» в качестве фундаментального понятия этого языка уже не может иметь места. Необходимо новое фундаментальное механическое понятие, на базе которого и должен строиться новый язык механики, более адекватный задачам описания космонавтики и мегамира.
Для того, чтобы найти это новое фундаментальное понятие, обратимся к космонавтике. В космонавтике «невесомость» есть центральное понятие.
Мы все легко можем определить наличие невесомости по телевизионной картинке. Но что это такое с точки зрения механической науки? Приведем лишь некоторые из определений невесомости из наиболее авторитетных источников..
Невесомость - состояние, когда сила взаимодействия тела с опорой (кажущийся вес тела), возникающая в связи с гравитационным притяжением или в связи с ускорением тела, исчезает. Иногда можно слышать другое название этого эффекта - микрогравитация.(Википедия ).
Определение просто невразумительное. Что за «сила взаимодействия в связи с ускорением»? Нет такого понятия в механике. А что такое «кажущийся вес»? И путать микрогравитацию с невесомостью вряд ли допустимо. Это разные понятия.
Невесомостью называется состояние, при котором действующие на тело гравитационные силы не вызывают взаимных давлений его частей друг на друга (Астрономический словарь на сайте Института космических исследований РАН) .
Вообще непонятно, почему вдруг «взаимные давления» внутри тела исчезают в космосе или у парашютиста в прыжке? Что, у него исчезает сердечное давление или клапан уже не давит на свое седло. Или исчезает внутреннее давление в жидкости, формирующее сферические капли в невесомости? И как определить, эти взаимные давления связаны с гравитационными силами или нет? И разве это соответствует телевизионной картинке с космического корабля? Даже самый малограмотный человек сразу скажет, что невесомость - это что-то совсем иное, а тем более сами космонавты.
Невесомость , - состояние тел вне сил притяжения (Русский орфографический словарь Российской академии наук).
Определение способно вызвать только улыбку. Но ведь создатели словаря - лингвисты - не сами это придумали, а пользовались, наверняка, консультацией специалистов из Академии наук.
Невесо мость - состояние материального тела, при котором действующие на него внешние силы или совершаемое им движение не вызывают взаимных давлений частиц друг на друга (Большая советская энциклопедия ).
Сопоставить как однопорядковое «силы» и «совершаемые движения» - это что-то лежащее за пределами механики. Заметим также, что во всех определениях имеется термин «состояние», хотя в механике нет понятия«состояние».
Таким образом, центральное понятие космонавтики - невесомость - в современной механике вообще не имеет сколько-нибудь корректного описания. Ощущение такое, что для теоретической механикиона «терра инкогнито», ворвавшаяся в сферу реальной механической практики, но для которой места в теории нет. Потому и сочиняют кто во что горазд.
Но если есть «невесомость», то должна быть и «весомость», отсутствие каковой создает «не-весомость». Таково требования научной логики, законов построения языков науки.
И для построения нового языка мы постулируем существование нового понятия механики - понятия «механического состояния механического объекта ». Этого понятия нет в механике Ньютона. Это новое концептуальное понятие для нового языка. И соответственно «весомость » есть характеристика механического состояния тела . А невесомость есть особый, частный случай весомого состояния, весомого состояния с отсутствующей весомостью.
Остается дать характеристику понятию весомость. Мы принимаем, что в новом языке механики весомость есть фундаментальное, неопределяемое в самом языке понятие, заменяющее фундаментальное понятие силы в ньютоновском языке. Весомость есть вектор, приложенный к самому телу и перемещающийся вместе с телом.
Мы не можем определить в самом языке понятие весомости, но зато можем дать описание устройств, которые измеряют эту величину. Эти измерители весомости мы будем называть «весомометрами ». Оказывается, весомометры широко используются в технике и, прежде всего, в космонавтике. Только носят они странное название «акселерометров », т.е. измерителей ускорений. Понятно, что никакого ускорения грузикна пружинке измерять не может (Академик Ишлинский поэтому предлагал для этих приборов название «ньютонометры», что лучше, но не совсем). Измеряет он не кинематическую характеристику - ведь последняя величина относительная и зависит от системы отсчета и наблюдателя, а именно характеристику механического состояния объекта. Есть и еще одно название у весомометров - это название «гравиметры », которое используется в гравиметрии. Это, во всяком случае, лучше, чем акселерометр. Заодно заметим, что человек (и иные животные) имеет орган чувства - шестой орган чувства - который состоит из целого набора весомометров. Этот орган чувства - вестибулярный аппарат - расположен во внутреннем ухе человека. Сами физиологические весомометры имеют некоторое медицинское название, но не имеют механического, ибо назвать эти внутренние физиологические весомометры акселерометрами у теоретиков-механиков не хватило духу, слишком это бы резало уши .
А связь неоптолемеевской механики с механикой Ньютона осуществляется через понятие силы . Нотеперь сила есть уже вторичное, производное понятие. Сила есть векторная величина пропорциональный произведению модуля весомости и массы тела и антиколлинеарный вектору весомости.
Здесь m - масса, W - вектор весомости, F - вектор силы. Вновь напомним, силы только электромагнитные, гравитационных нет. Так как к камню приложена сила опоры, направленная вверх, то весомость тел на Земле направлена вниз.
Отсюда сразу же видно, что с точки зрения ньютоновской механики весомость есть удельная сила, т.е. сила на единицу массы, правда, ориентированная в противоположную сторону по отношению к вектору силы.
И, наконец, уже не просто определение силы, а содержательная аксиома механики состоит в третьем законе Ньютона: сила реакции равна активной силе, но направлена в противоположную сторону.
Связь между движением и механическим состоянием в инерциальной системе отсчета в новой механике дается модифицированным Вторым законом (аксиомой) Ньютона : ускорение пропорционально весомости, но направление его обратно вектору весомости.
![]()
w – ускорение тела в инерциальной системе отсчета, W - его весомость. Получаем фундаментальный закон механики в очень простом виде. В это уравнение не входят никакие внутренние, имманентные характеристики тела. Это очень важно. Все тела движутся одинаково, если находятся в одинаковом механическом состоянии от какой-нибудь пылинки до снаряда главного калибра линкора.
В свое время Галилей, бросая камни с Пизанской башни, пришел к выводу, что все тела падают одинаково. Новый закон механики расширяет это утверждения до такого: все тела движутся одинаково, если находятся в одинаковом механическом состоянии.
В СИ единицей весомости является единица Н/кг. Эту единицу в гравиметрии принято называть Галилео, сокращенно Гл. Весомость на поверхности Земли 9.81 Гл, на поверхности Луны - 1.62 Гл, в ракете на участке выведения порядка 40 Гл, на боевом развороте в истребителе до 80 Гл, баллистической ракеты «Тополь-М» на взлете до 120 Гл, весомость пушечного снаряда при разгоне в канале ствола может составлять до 100 кГл., микрогравитационная весомость в орбитальной станции составляет порядка 1 нГл (наноГалилео). Мы видим, в каких больших пределах изменяется весомость, с которой имеет дело практика.
8.Весомика
Новая механика инициирует создание новой механической дисциплины - весомики . Это наука о механическом состоянии. Она найдет свое применение в самых различных прикладных науках и техниках. Это космическая, авиационная и морская медицина, биофизика, ветеринария, прочностные науки, спортивная медицина, механика спортивных дисциплин, механика и конструирование машин, аппаратов и парковых аттракционов и т.п. И прежде всего она даст всем этим наукам и техникам единую научною терминологию вместо каких-то странных «перегрузок», «недогрузок» и т.п.В новой механике весомика призвана занять такое же место, как статика в ньютоновской механике.
Итак, мы определили основные понятия нового механического языка. Если механический объект рассматривается как элементарный, неделимый, то он характеризуется единым вектором весомости, как и единой силой. Если же мы имеем составной механический объект, называемый телом, то имеем распределение весомости на теле. Это распределение может быть плоским, т.е. все части тела имеют одинаковую весомость. Но может быть и сложным, если тело совершает собственные движения, например, вращения или находится в негалилеевом пространстве.
9.Описание гравитационного поля
Итак, гравитационное поле есть область негалилеева пространства. Как же описать это пространство?
В ньютоновской механике есть гравитационные силы. Потому гравитация описывается напряженностью поля, т.е. распределением удельных гравитационный сил, сил, приложенных к единичной массе.
Но в новой механике нет гравитационных сил, а гравитация есть всего лишь свойство пространства. Поэтому ньютоновский подход не пригоден.
В гравитационном подходе Эйнштейна гравитация есть свойство, которое искривляет пространство. Это искривление приводит к тому, что координатная сетка (геодезические линии), которая в ОТО состоит из линий движения света, становится искривленной. Кривизна этого пространства и определяет гравитационное поле. Но ни в области космонавтики, ни в небесной механики, и даже в звездной и галактической механике это описание практически неприменимо. Слишком ничтожны в этих масштабах искривления световых траекторий и практические гравитационные поля для ОТО слишком малы. Использовать ОТО в области практически используемых гравитационных явлений то же самое, что использовать метровую рулетку для измерения атомных расстояний. В отличие от этого ньютоновский подход приводит к адекватным гравитационным характеристикам в масштабах космонавтики или небесной механики.
Итак, мы приходим к выводу: ньютоновский подход дает хорошее описание практически значимых гравитационных полей, но он основан на гравитационных силах, которых у нас нет, эйнштейновский подход основан на изменении свойств пространства, но он эффективен лишь в области сверхсильных гравитационных полей, ни в космонавтике, ни в небесной механике практически не встречающихся. Ему, возможно, есть место в космологии, но никак не в области описания полетов на околоземные орбиты или внутри Солнечной системы. А требуется создать описание гравитационного поля размерностно адекватное ньютоновскому, но при этом основывать это описание на изменении свойств пространства, как в эйнштейновском подходе.
И оказывается, это можно сделать. Для этого только нужно использовать фундаментальную величину новой механики - весомость.
В галилеевом пространстве можно создать инерциальную систему отсчета, в которой свободные тела движутся равномерно и прямолинейно или покоятся. Отсюда следует, что в галилеевом пространстве можно создать среду из покоящихся и невесомых тел. Но эта среда как раз и может быть системой отсчета. Нужно лишь эти покоящиеся невесомые тела определенным образом пометить, приписать им координаты, ииспользовать их для описания движений тел.
В негалилеевом пространстве свободные тела не могут быть неподвижны относительно друг друга. Любой ансамбль свободных тел начнет расползаться. А если мы хотим, чтобы тела в гравитационном поле были неподвижны друг относительно друга, их надо как-то скрепить друг с другом, т.е. приложить к ним силы. Причем, опять-таки, никакие не гравитационные, а обычные, электрической или магнитной природы.
Но если мы приложили к телам силы, то они уже перестают быть свободными и становятся уже весомыми. И в этой неподвижной среде существует распределение весомости. Это распределение весомости мы и можем использовать в качестве полевой характеристики гравитационного поля. Таким образом, именно поле весомости в неподвижной среде и может стать характеристикой гравитационного поля. Это распределение весомостей мы также можем назвать напряженностью гравитационного поля .
Легко видеть, что мы пришли численно к тому же самому ньютоновскому гравитационному полю, к удельной силе, только теперь ее переинтерпретировали:: не удельная сила тяготения, а удельная сила негравитационных сил, т.е. весомость, стала напряженностью гравитационного поля. Но значения напряженностей гравитационных полей в обеих теориях полностью совпадают.
Казалось бы, мыпришли к тому же самому, и никакой разницы в реальном описании гравитационных полей нет. Но не совсем. Дело в том, что гравитационная сила абсолютна, абсолютны силы, действующие между гравитирующими телами по закону всемирного тяготения. Потому гравитационного поля единственны и абсолютны. Они требует единственной и выделенной системы отсчета, т.е. коперникианской системы отсчета. Но в новой механике это есть распределение весомостей в жесткой виртуальной среде. А таких виртуальных сред можно ввести в пространстве сколько угодно. Нет априори выделенных сред.. Можно выбирать в качестве исходных тел различные тела, к которым и «прикреплять» другие тела с целью создания координатной среды. От абсолютного гравитационного поля мы приходим к многовариантному, относительному гравитационному полю. Так мы пришли к еще большей общей относительности гравитации, она оказывается «еще более относительной», чем это представлялось Эйнштейну.
Но эта относительность уже отнюдь не теоретический кунштюк для какой-то там «общей ковариантности». Она практична и необычайно важна для космонавтики. Например, мы можем в качестве исходного тела принять центр Земли и построить гравитационное поле в системе отсчета с неподвижным центром Земли. Космонавт на орбите может принять в качестве исходного тела свой корабль и построить систему отсчета с самим собой в качестве неподвижного начала отсчета и с соответствующим распределением весомостей в этой среде, каковая и будет гравитационным полем. Это космонавтоцентрицеское гравитационное поле будет существенно отличаться от геоцентрического.Конечно, необходимо еще открыть законы перехода от одного гравитационного поля к другому, и создать соответствующий математический аппарат,. Но это уже дело техническое. И космонавту в ряде случаев будет удобнее рассматривать движение тел в космонавтоцентрической системе отсчета. А лунонавту на лунной станции - в селеноцентрической системе отсчета, земному астроному - в геоцентрической (птолемеевской), а школьникам и студентам для наглядного представления строения Солнечной системы будет полезно использовать гелиоцентрическую систему. Таким образом, неоптолемеевская механика не отвергает коперникианскую, а всего лишь ставит ее в один ряд с другими системами отсчета, в том числе и птолемеевской. И вопрос, какая система правильная, вопрос, за который столько пролито крови и всходили на костры, оказался вопросом не религии или идеологии, а чистого прагматизма- какая система выгодней в той или иной задаче, такой и надо пользоваться. Новая механика объединяет Птолемея и Коперника, Джордано Бруно и его палачей.
При этом сразу же отметим, что все перечисленные выше системы отсчета связаны со свободными телами, потому все они локально галилеевы, т.е. в начале этих систем нет гравитационного поля, а напряженность поля нулевая.. Мы получили важнейшее свойство гравитационных полей, связанных со свободными телами, которого нет в нынешней механической теории, а вот практическая космонавтика ими пользуется давно. Но использование тех или иных схем и фактов без их теоретического обоснования нередко ведет к ошибкам и иным неблагоприятным результатам. Вот почему теоретическое обоснование космической практики важно.
10.Движение тел в гравитационном поле
А теперь мы можем записать и уравнение движения свободных тел в гравитационном поле. Это уравнение записывается очень просто: ускорение w свободного (невесомого) тела равно напряженности гравитационного поля V :
Каково ускорение свободного падения в поле Земли? Оно численно равно напряженности гравитационного поля на поверхности Земли и направлено в ту же сторону. Весомость на поверхности Земли нам известна, W =9.81 Гл. Но эта весомость есть одновременно и напряженность гравитационного поля на поверхности Земли, V =9.81 Гл. Отсюда и ускорение свободного падения численно равно напряженности поля, но имеет, естественно, другие единицы измерения - w =9.81 м/c 2 .
И, наконец, обобщенный закон движения весомого тела в гравитационном поле будет: ускорение весомого тела в гравитационном поле равно напряженности поля за минусом его весомости, т.е.
![]()
Мы получили обобщение Второго закона Ньютона. Он прекрасно объясняет все факты. Если тело неподвижно, ускорение равно нулю, то в гравитационном поле весомость равна напряженности поля и наоборот, напряженность гравитационного поля равна весомости неподвижных тел. Если гравитационного поля нет, то ускорение равно весомости тела с обратным знаком.А если есть гравитационное поле, а тело свободно, то его ускорение направлено вдоль напряженности поля и численно равно ему. Очень простая и наглядная интерпретация движений и состояний.
Заметим опять, никакие собственные, внутренние характеристики (например, масса) тела в это уравнение не входят. Важность этого для навигационных расчетов в космонавтике и вообще в механике трудно переоценить. Это еще большее расширение принципа Галилея: все тела в одном гравитационном поле и в одном механическом состоянии движутся одинаково.
11.Гармонические системы отсчета
Но сразу же отметим, что это уравнение получено не для произвольной системы отсчета, а лишь для специальных, так называемых, гармонических систем отсчета. Гармонической системой отсчета является система отсчета, которая инерциальна на бесконечности. Инерциальные системы отсчета являются, естественно, и гармоническими. Но неинерциальные системы отсчета в галилеевом пространстве уже негармоничны. В негалилеевом пространстве инерциальных систем не существует, но существуют системы отсчета, которые инерциальны за пределами области негалилеевости, т.е. на бесконечности. Это и есть гармонические системы отсчета. Если гравитацию «снять», то они превращаются в инерциальные системы отсчета. Например, система отсчета, связанная с Землей, ориентированная на удаленные звезды, не является инерциальной в связи с наличие поля Земли, но она гармонична. Поэтому проблема построения инерциальной системы отсчета на Земле формулируется не совсем верно. Это проблема построения гармонической системы отсчета. Она очень важна даже в бытовой жизни, например, для сотовой и космической связии систем космической навигации. Решаться она может либо по далеким звездам, либо через использование внутренних стабилизирующих устройств, например, гироскопов. Это также является важнейшей и постоянной задачей космонавтики.
Законы движения в негармонических, фактически, вращающихся системах отсчета усложняются, но на этом мы останавливаться не будем, так как наша задача не построение всей новой механики, а лишь демонстрация ее необходимости и формулировка тех основных понятий и законов, которые отличают ее от нынешней ньютоно-коперникианской механики. И вновь подчеркнем. Нынешняя механика не отвергается, она хороша и верна для круга явлений либо вне гравитационного поля, либо в постоянном гравитационном поле, т.е. в механике на поверхности Земли. Но в космонавтике, где имеется сложнейшее сочетание изменяющихся гравитационных полей и разнообразнейших движений, где объектом движения становятся не мертвые камни и космические тела, а мыслящее существо, человек, она неудовлетворительна.
12.Уравнения гравитационного поля
А теперь мы можем записать уравнения гравитационного (весомостного) поля. Это уравнение имеет вид идентичный полевому уравнению в ньютоновской механике:
![]()
Здесь r есть плотность вещества.
На первый взгляд это обычное уравнение ньютоновского гравитационного поля. Но здесь есть тонкости. Они следующие:
1.Полевое уравнение в механике Ньютона записывается в системе центра масс, т.е. в коперникианской системе отсчета. В нашей механике это уравнение верно для любой гармонической системы отсчета. Т.е. оно верно как для системы Солнца, так и в системе отсчета Земли и в системе отсчета орбитального или межпланетного корабля.
2.Из математики известно, что для решения этого уравнения необходимо задать или граничные, или начальные условия. Электромагнитное поле требует задания граничных условий. А вот гравитационное поле требует задания начальных. Граничные условия - нулевые условия на бесконечности для гармонической системы отсчета удовлетворяются автоматически. А начальные условия, т.е. напряженность поля в начале системы отсчета, т.е. весомость начального тела системы отсчета должны быть задано. И если начало системы отсчета связано со свободным телом, то эта система отсчета является локально инерциальной и начальное значение поля является нулевым. V (0)=0.
3.Из математики также известно, что для определения векторного поля задание одной дивергенции. недостаточно. Необходимо задать еще и ротор поля. Если принять, что гравитационное поле является потенциальным, то это означает, что ротор поля равен нулю и тогда система уравнений гравитационного поля в гармонической системе отсчета запишется в виде:
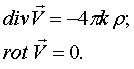
Таким образом, эта система полевых уравнений описывает гравитационное поле (поле весомости) в гармонической системе отсчета. Для негармонических систем отсчета распределение поля весомости будет иным, но об этом мы пока не будем распространяться.
13.Расширение гравитационной теории гравитации Ньютона
Существует ли расширение гравитационной теории? Мы имеем ввиду стандартный путь расширения путем добавления некоторых новых членов? Да. Для этого стоит ввести в правую часть второго уравнения ненулевой член. Так как уравнение аксиально-векторное, то и справа нужно внести какую-то аксиально-векторную характеристику среды. Есть такая? Да, это плотность собственного момента вращения (спина) s . И учитывая размерности, мы можем этот систему уравнений гравитационного поля в гармонической системе отсчета записать в виде:
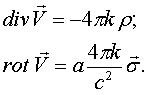
Здесь а - некоторая безразмерная константа, которую предстоит еще определить из наблюдений.
Что означает добавление этого члена? Это означает, что в окрестности вращающегося тела имеется дополнительная вихревая компонента гравитационного поля. Вихревое поле одиночного вращающегося тела подобно магнитному полю одиночного магнитного диполя. Оно спадает очень быстро, по кубу радиуса. И потому может оказывать влияние на движение только в ближайшей окрестности.
В ближайшей окрестности Солнца находится планета Меркурий. Несоответствие ее движения ньютоновским законам отмечено уже давно. И если считается, что это нашло свое отражение в эйнштейновской гравитационной теории, то почему это не может найти отражение и в модернизированной, неоньютоновской теории гравитации? Другой возможный эффект связан с воздействием этого поля на гироскоп в виде изменения оси его вращения.. И этот эффект, видимо, уже обнаружен в эксперименте на американском спутнике GP -B (гравитационный зонд – B ), запущенном в апреле 2004 года.
Возможны и иные проявления этого поля. При расчетах искривления света при прохождении его вблизи диска Солнца по ньютоновской теории (по этой теории все механические объекты движутся одинаково, движение определяется лишь начальными условиями) значение получается отличным от наблюдаемого. Вполне можно допустить, что это связано именно с влиянием вихревого поля Солнца. Вихревое поле будет особенно сильно влиять на движение газообразного и плазменного вещества в верхней оболочке Солнца. Вполне возможно, что это даст новые подходы в физике Солнца и солнечной атмосферы и ее активности. Вообще, вращение есть один из важнейших астрофизических факторов. И введение вихревой компоненты гравитационного поля может очень сильно изменить наши представления об устройстве мегамира. Образно говоря, если потенциальная компонента гравитационного поля обеспечивает устойчивость вселенной, то вихревая придает ему динамику. А ведь поразительную динамичность мы и наблюдаем в космосе, мегамире и даже на Земле.
14.Заключение
Прошлая (и нынешняя) ньютоно-коперникианская механика не отвечает требованиям, которые ставит перед механической теорией современная космонавтика. Она не дает космическому опыту адекватного теоретического описания,а нередко и просто ему противоречит. Только новая неньютоновская и некоперникианская механика позволит открыть перед космонавтикой и, даже более широко, перед механикой и ее практическими приложениями новые горизонты. В основе этой механики лежит новое понимание гравитации, гравитации без гравитационных сил, но, возможно, с вихревой компонентой.
Гравитационные силы описываются наиболее простыми количественными закономерностями. Но несмотря на эту простоту проявления сил тяготения могут быть весьма сложны и многообразны.
Гравитационные взаимодействия описываются законом всемирного тяготения, открытым Ньютоном:
Материальные точки притягиваются с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
Гравитационная постоянная. Коэффициент пропорциональности называется гравитациоутой постоянной. Эта величина характеризует интенсивность гравитационного взаимодействия и является одной из основных физических констант. Ее числовое значение зависит от выбора системы единиц и в единицах СИ равно Из формулы видно, что гравитационная постоянная численно равна силе притяжения двух точеных масс по 1 кг, расположенных на расстоянии друг от друга. Значение гравитационной постоянной столь мало, что мы не замечаем притяжения между окружающими нас телами. Только из-за огромной массы Земли притяжение окружающих тел к Земле решающим образом влияет на все, что происходит вокруг нас.
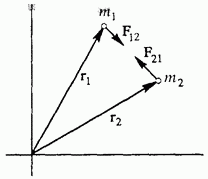
Рис. 91. Гравитационное взаимодействие
Формула (1) дает только модуль силы взаимного притяжения точечных тел. На самом деле речь в ней идет о двух силах, поскольку сила тяготения действует на каждое из взаимодействующих тел. Эти силы равны по модулю и противоположны по направлению в соответствии с третьим законом Ньютона. Они направлены вдоль прямой, соединяющей материальные точки. Такие силы называются центральными. Векторное выражение, например для силы с которой тело массы действует на тело массы (рис. 91), имеет вид
![]()
Хотя радиусы-векторы материальных точек зависят от выбора начала координат, их разность, а значит, и сила зависят только от взаимного расположения притягивающихся тел.
Законы Кеплера. К известной легенде о падающем яблоке, которое якобы навело Ньютона на мысль о тяготении, вряд ли следует относиться серьезно. При установлении закона всемирного тяготения Ньютон исходил из открытых Иоганном Кеплером на основании астрономических наблюдений Тихо Браге законов движения планет Солнечной системы. Три закона Кеплера гласят:
1. Траектории, по которым движутся планеты, представляют собой эллипсы, в одном из фокусов которых находится Солнце.
2. Радиус-вектор планеты, проведенный из Солнца, ометает за равные промежутки времени одинаковые площади.
3. Для всех планет отношение квадрата периода обращения к кубу большой полуоси эллиптической орбиты имеет одно и то же значение.
Орбиты большинства планет мало отличаются от круговых. Для простоты будем считать их точно круговыми. Это не противоречит первому закону Кеплера, так как окружность представляет собой частный случай эллипса, у которого оба фокуса совпадают. Согласно второму закону Кеплера движение планеты по круговой траектории происходит равномерно, т. е. с постоянной по модулю скоростью. При этом третий закон Кеплера говорит о том, что отношение квадрата периода обращения Т к кубу радиуса круговой орбиты одинаково для всех планет:
Движущаяся по окружности с постоянной скоростью планета обладает центростремительным ускорением, равным Воспользуемся этим, чтобы определить силу, которая сообщает планете такое ускорение при выполнении условия (3). Согласно второму закону Ньютона ускорение планеты равно отношению действующей на нее силы к массе планеты:
Отсюда, учитывая третий закон Кеплера (3), легко установить, как сила зависит от массы планеты и от радиуса ее круговой орбиты. Умножая обе части (4) на видим, что в левой части согласно (3) стоит одинаковая для всех планет величина. Значит, и правая часть, равная одинакова для всех планет. Поэтому т. е. сила тяготения обратно пропорциональна квадрату расстояния от Солнца и прямо пропорциональна массе планеты. Но Солнце и планета выступают в их гравитационном
взаимодействии как равноправные партнеры. Они отличаются друг от друга только массами. И поскольку сила притяжения пропорциональна массе планеты то она должна быть пропорциональна и массе Солнца М:
Вводя в эту формулу коэффициент пропорциональности G, который уже не должен зависеть ни от масс взаимодействующих тел, ни от расстояния между ними, приходим к закону всемирного тяготения (1).
Гравитационное поле. Гравитационное взаимодействие тел можно описывать, используя понятие гравитационного поля. Ньютоновская формулировка закона всемирного тяготения соответствует представлению о непосредственном действии тел друг на друга на расстоянии, так называемом дальнодействии, без какого-либо участия промежуточной среды. В современной физике считается, что передача любых взаимодействий между телами осуществляется посредством создаваемых этими телами полей. Одно из тел непосредственно не действует на другое, оно наделяет окружающее его пространство определенными свойствами - создает гравитационное поле, особую материальную среду, которая и воздействует на другое тело.
Представление о физическом гравитационном поле выполняет как эстетические, так и вполне практические функции. Силы тяготения действуют на расстоянии, они тянут там, где, мы едва ли можем увидеть, что именно тянет. Силовое поле представляет собой некоторую абстракцию, заменяющую нам крюки, веревочки или резинки. Никакой наглядной картины поля дать невозможно, поскольку само понятие физического поля относится к числу основных понятий, которые невозможно определить через другие, более простые понятия. Можно только описать его свойства.
Рассматривая способность гравитационного поля создавать силу, мы считаем, что поле зависит только от того тела, со стороны которого действует сила, и не зависит от того тела, на которое она действует.
Отметим, что в рамках классической механики (механики Ньютона) оба представления - о дальнодействии и взаимодействии через гравитационное поле - приводят к одинаковым результатам и в равной мере допустимы. Выбор одного из этих способов описания определяется исключительно соображениями удобства.
Напряженность поля тяготения. Силовой характеристикой гравитационного поля является его напряженность измеряемая силой, действующей на материальную точку единичной массы, т. е. отношением
Очевидно, что гравитационное поле, создаваемое точечной массой М, обладает сферической симметрией. Это значит, что вектор напряженности в любой его точке направлен к массе М, создающей поле. Модуль напряженности поля как следует из закона всемирного тяготения (1), равен
![]()
и зависит только от расстояния до источника поля. Напряженность поля точечной массы убывает с расстоянием по закону обратных квадратов. В таких полях движение тел происходит в соответствии с законами Кеплера.
Принцип суперпозиции. Опыт показывает, что гравитационные поля удовлетворяют принципу суперпозиции. Согласно этому принципу гравитационное поле, создаваемое какой-либо массой, не зависит от наличия других масс. Напряженность поля, создаваемого несколькими телами, равна векторной сумме напряженностей полей, создаваемых этими телами в отдельности.
Принцип суперпозиции позволяет рассчитывать гравитационные поля, создаваемые протяженными телами. Для этого нужно мысленно разбить тело на отдельные элементы, которые можно считать материальными точками, и найти векторную сумму напряженностей полей, создаваемых этими элементами. Пользуясь принципом суперпозиции, можно показать, что гравитационное поле, создаваемое шаром со сферически-симметричным распределением массы (в частности, и однородным шаром), вне этого шара неотличимо от гравитационного поля материальной точки такой же массы, как и шар, помещенной в центр шара. Это значит, что напряженность гравитационного поля шара дается той же формулой (6). Этот простой результат приводится здесь без доказательства. Оно будет дано для случая электростатического взаимодействия при рассмотрении поля заряженного шара, где сила также убывает обратно пропорционально квадрату расстояния.
Притяжение сферических тел. Используя этот результат и привлекая третий закон Ньютона, можно показать, что два шара со сферически-симметричным распределением масс у каждого притягиваются друг к другу так, как если бы их массы были сосредоточены в их центрах, т. е. просто как точечные массы. Приведем соответствующее доказательство.
Пусть два шара массами притягивают друг друга с силами (рис. 92а). Если заменить первый шар точечной массой (рис. 92б), то создаваемое им гравитационное поле в месте расположения второго шара не изменится и, следовательно, не изменится сила действующая на второй шар. На основании третьего
закона Ньютона отсюда можно сделать вывод, что второй шар действует с одной и той же силой как на первый шар, так и на заменяющую его материальную точку Эту силу легко найти, учитывая, что создаваемое вторым шаром гравитационное поле в том месте, где находится первый шар, неотличимо от поля точечной массы помещенной в его центр (рис. 92в).
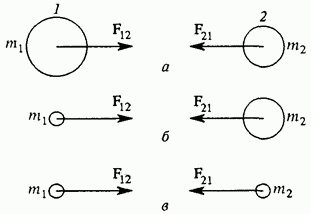
Рис. 92. Сферические тела притягиваются друг к другу так, как если бы их массы были сосредоточены в их центрах
Таким образом, сила притяжения шаров совпадает с силой притяжения двух точечных масс ту и расстояние между которыми равно расстоянию между центрами шаров.
Из этого примера наглядно видна практическая ценность концепции гравитационного поля. В самом деле, было бы очень неудобно описывать силу, действующую на один из шаров, как векторную сумму сил, действующих на отдельные его элементы, учитывая при этом, что каждая из этих сил, в свою очередь, представляет собой векторную сумму сил взаимодействия этого элемента со всеми элементами, на которые мы должны мысленно разбить и второй шар. Обратим внимание еще и на то, что в процессе приведенного доказательства мы поочередно рассматривали в качестве источника гравитационного поля то один шар, то другой, в зависимости от того, интересовала ли нас сила, действующая на тот или на другой шар.
Согласно второму закону Ньютона равно Видно, что оно направлено к центру Земли и в соответствии с (7) по модулю равно
![]()
Но правая часть (8) дает значение напряженности гравитационного поля Земли вблизи ее поверхности. Итак, напряженность гравитационного поля и ускорение свободного падения в этом поле - это одно и то же. Именно поэтому мы сразу обозначили эти величины одной буквой
Взвешивание Земли. Остановимся теперь на вопросе об экспериментальном определении значения гравитационной постоянной Прежде всего отметим, что его нельзя найти из астрономических наблюдений. Действительно, из наблюдений за движением планет можно найти только произведение гравитационной постоянной на массу Солнца. Из наблюдений за движением Луны, искусственных спутников Земли или за свободным падением тел вблизи земной поверхности можно найти только произведение гравитационной постоянной на массу Земли. Для определения необходимо иметь возможность независимо измерить массу источника гравитационного поля. Это можно сделать только в опыте, производимом в лабораторных условиях.
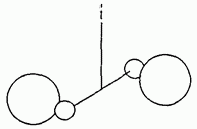
Рис. 93. Схема опыта Кавендиша
Такой опыт был впервые выполнен Генри Кавендишем в с помощью крутильных весов, к концам коромысла которых были прикреплены небольшие свинцовые шары (рис. 93). Вблизи от них закреплялись большие тяжелые шары. Под действием сил притяжения малых шаров к большим коромысло крутильных весов немного поворачивалось, и по закручиванию упругой нити подвеса измерялась сила. Для интерпретации этого опыта важно знать, что шары взаимодействуют так же, как и соответствующие материальные точки такой же массы, ибо здесь в отличие от планет размеры шаров Нельзя считать малыми по сравнению с расстоянием между ними.
В своих опытах Кавендиш получил значение гравитационной постоянной всего на отличающееся от принятого в настоящее время. В современных модификациях опыта Кавендиша производится измерение ускорений, сообщаемых малым шарам на коромысле гравитационным полем тяжелых шаров, что позволяет повысить точность измерений. Знание гравитационной постоянной позволяет определить массы Земли, Солнца и других источников тяготения по наблюдениям за движением тел в создаваемых ими гравитационных полях. В этом смысле опыт Кавендиша иногда образно называют взвешиванием Земли.
Всемирное тяготение описывается очень простым законом, который, как мы видели, легко устанавливается на основе законов Кеплера. В чем же величие открытия Ньютона? В нем нашла воплощение идея о том, что падение яблока на Землю и движение Луны вокруг Земли, которое тоже в известном смысле представляет собой падение на Землю, имеют общую причину. В те далекие времена это была удивительная мысль, поскольку общая мудрость гласила, что небесные тела движутся по своим «совершенным» законам, а земные объекты подчиняются «мирским» правилам. Ньютон пришел к мысли о том, что единые законы природы справедливы для всей Вселенной.
Введите такую единицу силы, чтобы в законе всемирного тяготения (1) значение гравитационной постоянной С равнялось единице. Сравните эту единицу силы с ньютоном.
Существуют ли отклонения от законов Кеплера для планет Солнечной системы? Чем они обусловлены?
Как из законов Кеплера установить зависимость силы тяготения от расстояния?
Почему гравитационную постоянную нельзя определить на основе астрономических наблюдений?
Что такое гравитационное поле? Какие преимущества дает описание гравитационного взаимодействия с помощью понятия поля по сравнению с представлением о дальнодействии?
В чем заключается принцип суперпозиции для гравитационного поля? Что можно сказать о гравитационном поле однородного шара?
Как связаны между собой напряженность гравитационного поля и ускорение свободного падения?
Рассчитайте массу Земли М, используя значения гравитационной постоянной радиуса Земли км и ускорения свободного падения
Геометрия и тяготение. С простой формулой закона всемирного тяготения (1) связано несколько тонких моментов, заслуживающих отдельного обсуждения. Из законов Кеплера следует,
что расстояние в знаменатель выражения для силы тяготения входит во второй степени. Вся совокупность астрономических наблюдений приводит к выводу, что значение показателя степени равно двум с очень высокой точностью, а именно Этот факт в высшей степени замечателен: точное равенство показателя степени двум отражает евклидову природу трехмерного физического пространства. Это значит, что положение тел и расстояние между ними в пространстве, сложение перемещений тел и т. д. описывается геометрией Евклида. Точное равенство двум показателя степени подчеркивает то обстоятельство, что в трехмерном евклидовом мире поверхность сферы точно пропорциональна квадрату ее радиуса.
Инертная и гравитационная массы. Из приведенного вывода закона тяготения следует также, что сила гравитационного взаимодействия тел пропорциональна их массам, а точнее - инертным массам, фигурирующим во втором законе Ньютона и описывающим инертные свойства тел. Но инертность и способность к гравитационным взаимодействиям представляют собой совершенно разные свойства материи.
В определении массы на основе инертных свойств используется закон . Измерения массы в соответствии с этим ее определением требуют проведения динамического эксперимента - прикладывается известная сила и измеряется ускорение. Именно так с помощью масс-спектрометров определяются массы заряженных элементарных частиц и ионов (а тем самым и атомов).
В определении массы на основе явления тяготения используется закон Измерение массы в соответствии с таким определением производится с помощью статического эксперимента - взвешиванием. Тела располагают неподвижно в гравитационном поле (обычно это поле Земли) и сравнивают действующие на них силы тяготения. Определенная таким образом масса называется тяжелой или гравитационной.
Будут ли значения инертной и гравитационной масс одинаковыми? Ведь количественные меры этих свойств в принципе могли бы быть различными. Впервые ответ на этот вопрос был дан Галилеем, хотя он, по-видимому, и не подозревал об этом. В своих опытах он намеревался доказать, что неверны господствовавшие тогда утверждения Аристотеля о том, что тяжелые тела падают быстрее легких.
Гравитационные массы тел пропорциональны их инертным массам. Надлежащим выбором единиц их можно сделать просто равными.
Совпадение значений инертной и гравитационной масс подтверждалось много раз со все возрастающей точностью в разнообразных опытах ученых разных эпох - Ньютона, Бесселя, Этвеша, Дикке и, наконец, Брагинского и Панова, которые довели относительную погрешность измерений до . Чтобы лучше представить себе чувствительность приборов в таких опытах, отметим, что это эквивалентно возможности обнаружить изменение массы теплохода водоизмещением в тысячу тонн при добавлении к нему одного миллиграмма.
В ньютоновской механике совпадение значений инертной и гравитационной масс не имеет под собой физической причины и в этом смысле является случайным. Это просто экспериментальный факт, установленный с очень высокой точностью. Если бы это было не так, ньютоновская механика ничуть не пострадала бы. В созданной Эйнштейном релятивистской теории тяготения, называемой также общей теорией относительности, равенство инертной и гравитационной масс имеет принципиальное значение и изначально заложено в основу теории. Эйнштейн предположил, что в этом совпадении нет ничего удивительного или случайного, ибо в действительности инертная и гравитационная массы представляют собой одну и ту же физическую величину.
Почему значение показателя степени, в которой расстояние между телами входит в закон всемирного тяготения, связано с евклидовостью трехмерного физического пространства?
Как определяются инертная и гравитационная массы в механике Ньютона? Почему в некоторых книгах даже не упоминается об этих величинах, а фигурирует просто масса тела?
Предположим, что в некотором мире гравитационная масса тел никак не связана с их инертной массой. Что можно было бы наблюдать при одновременном свободном падении разных тел?
Какие явления и опыты свидетельствуют о пропорциональности инертной и гравитационной масс?